"How Can I Find The Mean And" is a question often asked in statistics, mathematics, and probability. The mean is a measure of the central tendency of a dataset, representing an average value.
Calculating the mean is crucial for analyzing data, summarizing observations, and understanding the overall trend within a dataset. Throughout history, the concept of mean has played a vital role in statistics, with ancient Greek philosophers and mathematicians contributing to its development.
This article delves into the intricacies of finding the mean, exploring various methods applicable to different types of datasets. We'll examine the importance of mean in data interpretation and its significance in statistical analysis.
- Unraveling The Enigmatic Kertia Marley Discoveries And Insights
- Unveiling The Heartwarming World Of Ellen Pompeos Family A Journey Of Love And Resilience
- Unveiling The Talent Of Johvonnie Jacksons Daughter Yasmin
- Unveiling The World Of Liz Wheelers Husband Uncover Hidden Truths And Intriguing Insights
- Unveiling The Legacy And Expertise Of Greg Collinsworth A Journey Of Gridiron Greatness
How Can I Find the Mean And
To fully understand the concept of finding the mean, it is crucial to grasp its essential aspects and their interconnections.
- Dataset: Collection of numerical values
- Central Tendency: Measure of the typical value
- Average Value: Sum of all values divided by the number of values
- Data Analysis: Summarizing and interpreting data
- Statistical Analysis: Drawing conclusions from data
- Arithmetic Mean: Sum of values divided by the number of values
- Weighted Mean: Average considering the importance of each value
- Geometric Mean: nth root of the product of n values
- Harmonic Mean: Inverse of the average of the inverses
- Median: Middle value of a dataset
These aspects are interconnected, providing a comprehensive understanding of finding the mean. Together, they enable us to analyze data effectively, make informed decisions, and draw meaningful conclusions from numerical information.
Dataset
A dataset is a crucial component of finding the mean. It represents the collection of numerical values upon which statistical calculations are performed. Without a dataset, calculating the mean is impossible.
- Unveiling Sara Matter Discoveries And Insights In Patientcentered Care
- Unveiling The Visionary Vince Mcmahon Srs Unforgettable Legacy In Wrestling
- Uncover The Story Behind Ray Lewiss Enduring Love And Support
- Unlocking Gender Equality Unveiling The Secrets Of The Rajek Model
- Unveiling The Inspiring Story Of Ray Lewiss Remarkable Children
The relationship between dataset and mean is causal. The availability of a dataset determines whether the mean can be calculated. For instance, if you want to find the mean of students' test scores, you need a dataset containing those scores. Without the dataset, you cannot proceed with the calculation.
In real-world applications, datasets are ubiquitous. Market researchers collect survey data to determine consumer preferences, scientists gather experimental data to test hypotheses, and businesses analyze sales figures to make informed decisions. In each case, the dataset is essential for calculating the mean, which serves as a summary measure of the data.
Understanding this connection is vital for data analysis and interpretation. By recognizing the importance of the dataset in calculating the mean, we can ensure that our statistical analyses are based on complete and accurate information. This understanding empowers us to make informed decisions based on reliable data.
Central Tendency
Central tendency measures the "typical" value of a dataset, providing a concise summary of the data's central location. It is a crucial component of "How Can I Find The Mean And" because the mean is one of the most common measures of central tendency.
The mean, also known as the average, is calculated by summing all values in a dataset and dividing the sum by the number of values. It represents a balance point of the data, where half of the values are above the mean and half are below. The mean is particularly useful when the data is normally distributed, as it provides a reliable estimate of the data's center.
In real-life applications, central tendency plays a vital role in various fields. For instance, in finance, the mean return rate of an investment portfolio is used to assess overall performance. In education, the mean score of a standardized test indicates the average performance of students. Understanding central tendency and its connection to finding the mean empowers us to interpret data effectively and make informed decisions.
Average Value
The average value, calculated by summing all values in a dataset and dividing the sum by the number of values, is a critical component in finding the mean. The mean, a measure of central tendency, represents the typical value of a dataset. Understanding this relationship is fundamental in statistics and data analysis.
The average value directly contributes to finding the mean, acting as its foundation. To calculate the mean, one must first determine the average value of the given dataset. This average value serves as the basis for further calculations, providing a central point around which the data is distributed.
In real-life applications, the connection between average value and mean is evident in various scenarios. For instance, in calculating the average household income, the total income of all households is summed and then divided by the number of households. This average value provides an overall representation of the central tendency of household incomes.
Grasping this connection empowers us to effectively analyze and interpret data. By understanding how the average value contributes to finding the mean, we can make informed decisions based on reliable data summaries and gain valuable insights into the underlying patterns and trends within datasets.
Data Analysis
Within the context of "How Can I Find The Mean And," data analysis plays a crucial role in summarizing and interpreting the underlying data to uncover meaningful insights. It involves examining, organizing, and presenting data in a way that allows for effective decision-making.
- Data Summarization
Data summarization condenses large datasets into manageable and meaningful statistics, such as the mean, median, and mode. These summary measures provide a concise overview of the data's central tendencies and variability.
- Data Visualization
Data visualization presents data in visual formats, such as charts and graphs, to make complex information more accessible and easier to understand. Visualizing the data helps identify patterns, trends, and outliers.
- Statistical Inference
Statistical inference uses sample data to make predictions about the larger population. By drawing conclusions from a representative sample, researchers can gain insights into the characteristics of the entire population.
- Data Interpretation
Data interpretation involves drawing meaningful conclusions from the analyzed data. It requires an understanding of the context, biases, and limitations of the data to make informed judgments and recommendations.
These facets of data analysis are interconnected and essential for finding the mean. By effectively summarizing, visualizing, and interpreting data, researchers can accurately calculate the mean and gain valuable insights into the underlying dataset.
Statistical Analysis
Within the context of "How Can I Find The Mean And," statistical analysis plays a pivotal role in drawing meaningful conclusions from numerical data. It involves applying statistical techniques to make informed inferences about the larger population based on a representative sample.
- Hypothesis Testing
Hypothesis testing allows researchers to evaluate the validity of claims or assumptions about a population. By formulating a hypothesis, collecting data, and conducting statistical tests, they can determine whether the data supports or refutes the hypothesis.
- Confidence Intervals
Confidence intervals provide a range of values within which the true population mean is likely to fall. This range is calculated based on the sample mean, sample size, and a desired level of confidence.
- Regression Analysis
Regression analysis investigates the relationship between a dependent variable and one or more independent variables. It allows researchers to model the impact of independent variables on the dependent variable and make predictions about future outcomes.
- Data Mining
Data mining involves extracting hidden patterns, correlations, and trends from large datasets. By applying statistical algorithms, researchers can uncover valuable insights and make informed decisions based on the discovered knowledge.
These facets of statistical analysis are intricately connected to finding the mean. By drawing conclusions from data, researchers can assess the significance of the mean, make inferences about the population, and gain a deeper understanding of the underlying relationships within the dataset. The insights gained through statistical analysis empower data-driven decision-making and contribute to the advancement of various fields.
Arithmetic Mean
Within the broader context of "How Can I Find The Mean And," the arithmetic mean, calculated by summing all values and dividing by the number of values, plays a central role as one of the most commonly used measures of central tendency.
- Additivity
The arithmetic mean adheres to the property of additivity, meaning that the mean of a sum of independent random variables equals the sum of their means.
- Linearity
The arithmetic mean exhibits linearity, implying that a constant factor can be moved outside the mean operation without altering the result.
- Stability
The arithmetic mean is a stable statistic, meaning that it is not easily affected by outliers or extreme values within the dataset.
- Interpretability
The arithmetic mean has a straightforward interpretation as the average value of the dataset, making it easy to understand and communicate its significance.
These facets of the arithmetic mean highlight its strengths and limitations as a measure of central tendency. Its additivity and linearity properties make it particularly useful in statistical modeling and analysis. Its stability ensures reliability even in the presence of outliers. However, its sensitivity to extreme values should be considered when interpreting the mean.
Weighted Mean
Within the context of "How Can I Find The Mean And," the weighted mean emerges as a crucial component, offering a refined approach to calculating the mean by considering the relative significance or importance of each data point.
Unlike the arithmetic mean, which treats all values equally, the weighted mean assigns varying weights to different data points based on their perceived level of importance. This weighted average is then calculated by summing the products of each data point and its corresponding weight, and dividing the result by the sum of all weights. The weighted mean is particularly useful when dealing with datasets where certain values hold greater influence or significance than others.
In real-life applications, the weighted mean finds numerous practical applications. For instance, in market research, survey responses may be weighted based on demographic factors to ensure representativeness of the target population. In finance, investment portfolios may be weighted according to risk tolerance or expected returns. By incorporating the importance of each data point, the weighted mean provides a more accurate and nuanced representation of the central tendency.
Geometric Mean
Within the realm of "How Can I Find The Mean And," the geometric mean emerges as a specialized measure of central tendency, offering unique advantages in certain scenarios. Defined as the nth root of the product of n values, the geometric mean captures the typical value of a dataset while considering the multiplicative relationships between data points.
- Multiplicative Property
Unlike the arithmetic mean, which is sensitive to outliers, the geometric mean is less affected by extreme values due to its multiplicative nature.
- Growth Rates
The geometric mean is particularly useful for analyzing growth rates or percentage changes over time, as it reflects the average percentage change.
- Financial Applications
In finance, the geometric mean is employed to calculate average returns on investments, providing a more accurate representation of compounded growth.
- Biological Applications
In biology, the geometric mean is used to measure the average size of cells or organisms, as it accounts for the multiplicative nature of cell division or growth.
These facets of the geometric mean highlight its strengths and limitations in relation to "How Can I Find The Mean And." Its multiplicative property and resilience to outliers make it suitable for specific applications, while its focus on multiplicative relationships distinguishes it from other measures of central tendency.
Harmonic Mean
The harmonic mean is another measure of central tendency that finds applications in a variety of fields, including statistics, physics, and economics. It is defined as the inverse of the average of the inverses of a given set of numbers. In other words, if we have a set of numbers, x1, x2, ..., xn, then the harmonic mean (HM) is given by:
HM = n / (1/x1 + 1/x2 + ... + 1/xn)
The harmonic mean is often used to calculate the average of rates or ratios. For example, if we have a set of speeds, we can use the harmonic mean to calculate the average speed. The harmonic mean is also used in physics to calculate the average resistance of a set of resistors connected in parallel.
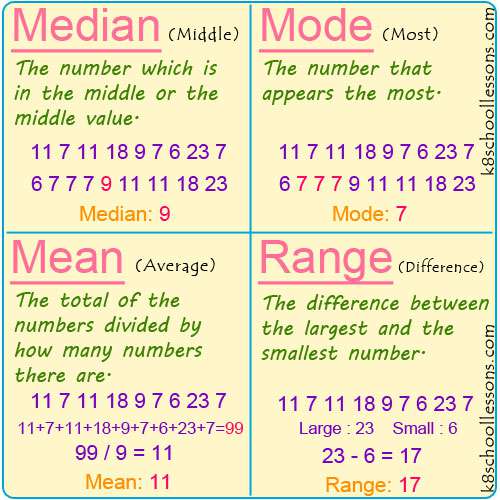
Median
Within the realm of "How Can I Find The Mean And," the median emerges as a crucial measure of central tendency, offering unique insights and applications. Distinct from the mean, the median is not affected by extreme values and provides a more robust measure of the "typical" value in a dataset.
- Positional Definition
The median is defined as the middle value of a dataset, when assorted in ascending or descending order. It divides the dataset into two equal halves, with half of the values being greater than or equal to the median and the other half being less than or equal to the median.
- Robustness to Outliers
Unlike the mean, the median is not swayed by extreme values or outliers. It remains a stable measure even in the presence of data points that deviate significantly from the rest of the dataset.
- Real-Life Applications
The median finds practical applications in various fields. In economics, it is used to calculate the median income, which provides a more representative measure of the typical income level compared to the mean, which can be distorted by high earners.
- Comparison to the Mean
In symmetric datasets, the median and mean often coincide. However, in skewed datasets, the median provides a more reliable measure of central tendency as it is not pulled towards the extreme values like the mean.
By understanding these facets of the median, we gain a deeper appreciation of its role in statistical analysis and its advantages in certain scenarios. Whether seeking a robust measure unaffected by outliers or a better representation of the typical value in skewed datasets, the median stands as a valuable tool in the context of "How Can I Find The Mean And."
Through this in-depth exploration of "How Can I Find The Mean And," we have gained a comprehensive understanding of the various measures of central tendency and their applications. The mean, weighted mean, geometric mean, harmonic mean, and median each offer unique insights into the "typical" value of a dataset, depending on factors such as data distribution, outliers, and the desired emphasis on specific data points.
The key takeaway is that choosing the appropriate measure of central tendency is crucial for accurate data analysis and interpretation. The mean provides an overall average, the weighted mean considers the importance of each data point, the geometric mean captures multiplicative relationships, the harmonic mean is useful for rates and ratios, and the median offers robustness against outliers. Understanding the interconnections between these measures empowers us to make informed decisions and draw meaningful conclusions from data.
Related Resources:
- Unveiling The Paige Green Age Discoveries And Insights Await
- Unveiling Robert Redfords Relationship History Insights And Revelations
- Unveiling The Truth Jimmy Kimmels Firing Rumors Debunked
- Unveiling The Age Enigma Preston Bezos And His Connection To Jeff Bezos
- Unveiling The Enigmatic Lori Petty Discoveries And Insights
Detail Author:
- Name : Prof. Ashley Steuber
- Username : schulist.gerhard
- Email : gturcotte@wuckert.com
- Birthdate : 2006-04-20
- Address : 1634 Swift Roads North Mittie, DE 98843
- Phone : +1.253.637.4726
- Company : Mohr LLC
- Job : Material Movers
- Bio : Nulla nam numquam nostrum reiciendis. Sed optio nulla veniam sunt consequatur. Facilis aut aliquid voluptatibus nesciunt amet.
Socials
tiktok:
- url : https://tiktok.com/@mrazh
- username : mrazh
- bio : Veritatis doloremque ut voluptatem molestiae facere sit sunt.
- followers : 5422
- following : 696
instagram:
- url : https://instagram.com/mrazh
- username : mrazh
- bio : Quia tempora sint quisquam ea iste laboriosam. Culpa perspiciatis sed voluptas numquam.
- followers : 1665
- following : 1825
linkedin:
- url : https://linkedin.com/in/hayley_xx
- username : hayley_xx
- bio : Non qui magni ipsa praesentium deleniti adipisci.
- followers : 3946
- following : 2369